I work in a big office. One of the things about a big office is that there are a lot of toilets. Now I am as communally-minded as the next man (this is assuming that the next man is a reclusive hermit living on a remote Scottish island), but I do like to maintain a degree of privacy when it comes to most bodily functions. In a toilet, this privacy translates as a good urinal’s distance between myself and any fellow occupants.
Now, as I have stated, where I work there are a lot of toilets. Ones with two urinals; ones with three urinals; ones with four urinals; even ones with five urinals.




To work out which one of these toilets affords me the best chance of the privacy I require, I have been required to fall back on a bit of basic probability. It all comes down to where in the line is the position of the urinal you select. A few simple diagrams may help to explain:
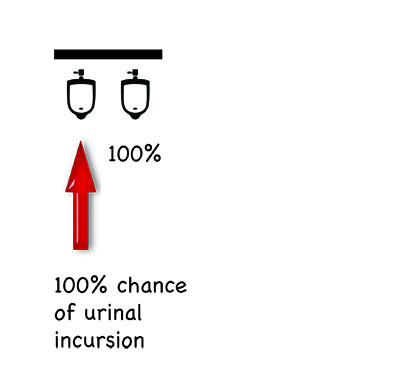
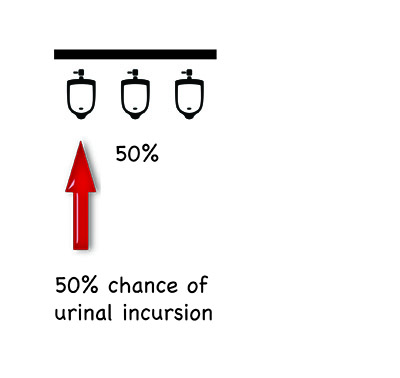
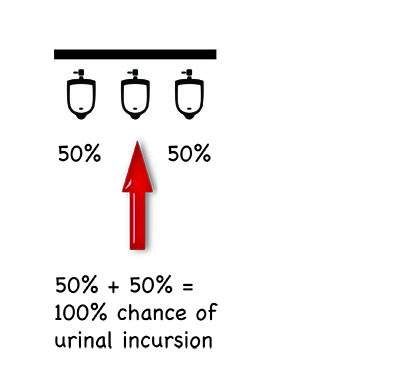
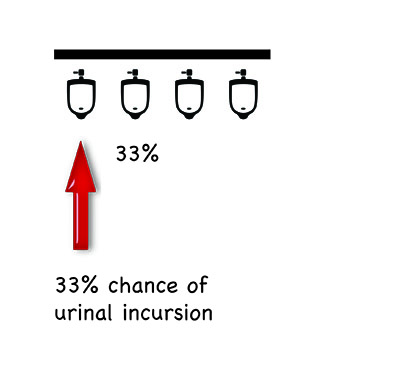
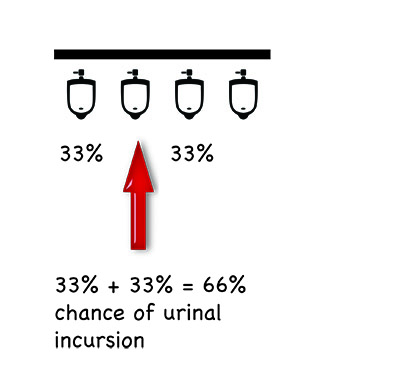
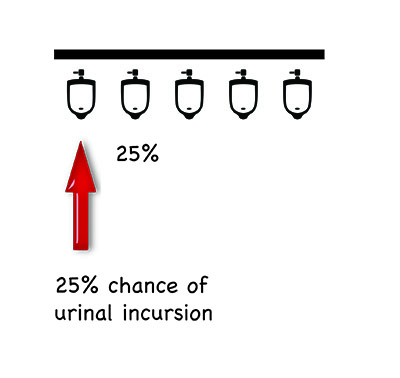
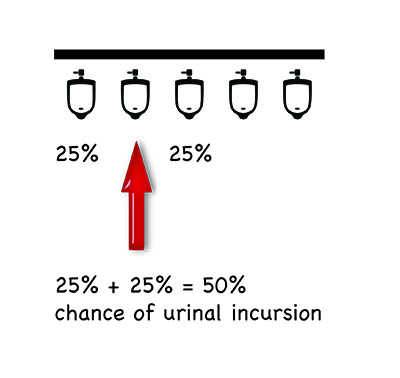
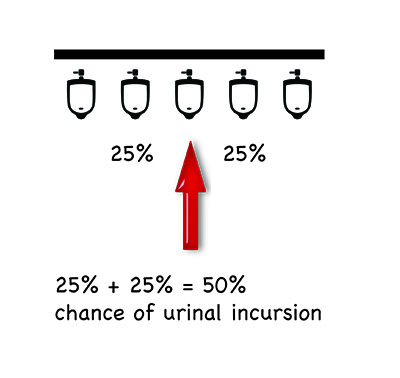
Of course, these are only the most basic permutations. Mathematical matters and privacy conundrums become considerably more complicated if someone already occupies one of the urinals before you; if more than one person comes in after you; if you factor in human bias. In fact, the range of possibilities is staggering.
I think I’ll just sit down here for a little bit while I try to work things out.

© Simon Turner-Tree

Sometimes Simon Turner-Tree just wants to be on his own.

[…] Discover some of the other things Simon gets up to in the company washroom in Urinals: a Basic Lesson in Probability. […]
LikeLike
[…] attentive followers of my writings will know that one thing I appreciate is a measure of privy privacy, so it should be safe to assume that in the Gents’ Toilet at Broadstairs Railway Station I have […]
LikeLike
[…] started when I worked out the probability of encountering a neighbour-free urinal at my workplace; it continued when I stumbled upon the mind-bogglingly spacious toilets at Broadstairs Railway […]
LikeLike